I. 애니메이션에 많이 나오는 구타를 당하니까 슝 하고 날아가서 반짝반짝 꺼지는 듯한 연출을 하려면 얼마나 세게 쳐야 하는지 계산해봤다.
I. 애니메이션에 많이 나오는 구타를 당하니까 슝 하고 날아가서 반짝반짝 꺼지는 듯한 연출을 하려면 얼마나 세게 쳐야 하는지 계산해봤다.

남의 갈기질.png”
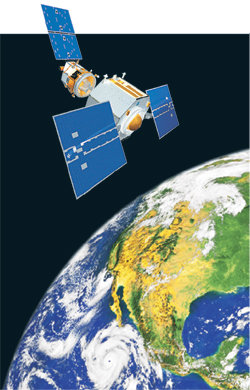
I. 일단 몇 가지 가정을 하면서 시작하자. 주먹으로 사람을 찢을 때 주먹을 몸에 바짝 붙인 채 충돌을 시작해 팔을 뻗는다고 가정하고 이때 상대방에게 가해지는 힘은 일정하다고 하자. 이를 가지고 몇 가지 공식을 유도할 수 있다. $2aS=V^2-V_0^2$2aS=V2−V20$2\cdot \frac{F}{m+M}\cdot l=V^2$2·Fm+M·l=V2
이때 m은 상대의 체중, M은 팔의 질량, l은 팔의 길이, V는 최종 속도이다.이때 최종 속도로 지구 탈출 속도를 대입하고 힘에 대해 정리하면 $2\cdot\frac{F}{m+M}\cdotl=11200^2$2·Fm+M·l=112002$F=\frac{11200^2\left(m+M\right)}{2l}$F=112002(m+M)2l

가 된다. 따라서 우리는 앞으로 얼마나 많은 힘을 가해야 할지 계산할 수 있다. 하지만 이것으로 인간의 피해를 계산하기는 쉽지 않다.따라서 이제는 이를 가속도 측면에서 분석해 볼 것이다.첫 번째 식에서 가속도를 F/m로 대체하지 않고 계산하면 $a=\frac{11200^2}{2l}$a=1120022l
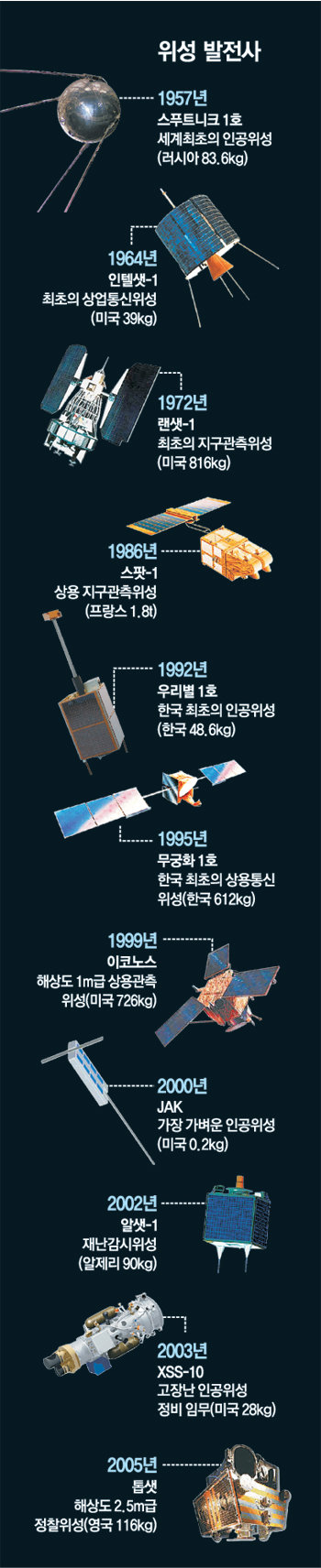
의 다소 간결한 식이 되다.이것을 이용해 「가속시킨다」가 아니라 「중력의 영향을 받는다」라고 생각하면, 다음과 같다.

인간이 주먹 모양의 빨랫대에 널려 있는 모습이다

이 인간은 ma의 힘을 받고 있다.이 상태와 위의 계산식에 ‘-(울음)’을 본격적으로 대입하여 계산하면 다음과 같은 수가 나온다: 100kg인 사람이 팔길이 60cm, 팔무게 5.7kg인 사람에게 복부를 맞는 경우-힘: 110491733N, 가속도: 1045333m/s2의 엄청난 힘을 내야 한다.이를 항성 중력에 비해 설명해 본다. $F=\frac{G·M·m}{R^2}$F=G·M·mR2
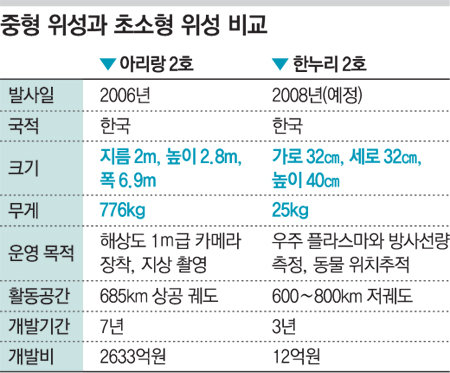
이 중력 공식을 변형하고 태양 반경의 때에 이런 힘을 내는 천체의 질량을 요구하자:$\frac<G·M·m}{R^2}=mg$G·M·mR2=mg-g=\frac<G·M}{R^2}$g=G·MR2$=\frac<6.67384\cdot 10^{-11}\cdot M}{696340^2}$=6.67384·10− 11·M6963402$\therefore\104533333=\frac<6.67384\cdot 10^{-11}\cdot M}{696340^2}$∴ 104533333=6.67384·10− 11·M6963402$M=\frac<104533333\cdot 696340^2}{6.6384\cdot 10^{-11}}$M=104533333·69634026.6384·10−11$=7.63544\cdot 10^{29}\left(kg\right)$=7.63544·1029(kg)

이는 태양 질량의 절반 정도다.너무 오랜만에 작성하는 블로그 글이기도 하고, 무작정 글을 쓰다 보니 글의 내용이 빈약해진 것 같아 안타깝다. 다음에는 이것을 좀 더 다듬어 2탄으로 돌아오도록 하겠다.

